Consensus Problem

在分布式系统中，一致性问题的解决是众多分布式算法得以工作的前提条件。这里所说的解决依赖于对系统模型的假设，事实上即便是在工业界得到广泛使用的著名的Paxos算法，也不能完全地解决一致性问题。

Importance

一致性问题是具有普遍意义的。举例来说，一个leader选举算法的safty属性要求算法结束时，所有节点公认某个一致的节点作为其leader；再比如，在一个分布式数据库系统中，某个数据具有多个拷贝，当数据发生变化时，所有这些拷贝都需要做出一致的调整(ACID中的C)。

Simplified Version

通常，研究一致性问题采用一个简化模型：

• 可能存在节点fail
• 节点间两两均可通信，通信的信道是可靠的
• 系统中的N个节点各自有一个1bit的初始状态 (0/1)
• 各个节点之间以消息的方式来改变彼此的状态
  • 通信可以有同步模型和异步模型之分
• 每个节点根据当前状态和接收到的消息唯一确定下一个状态
• 最终，每个正常工作的节点具有相同的状态 (0/1)
  • 总是全0或者总是全1的平凡解没有意义

很显然如果这个简单版本的一致性问题无法得到解决，那么一般意义上的一致性问题亦然。

Solution for Synchronous System

同步模型的假设下，一致性问题有较好的解决：

• 同步模型，每个消息的时延具有上限，以这个上限为间隔来划分轮数
• 假设系统最多有f个节点fail
• 每一轮中，每个节点将自己“已见过的状态值”广播给所有节点
• 每个节点在接收到消息后将其中的状态值合并入“已见过的状态值”集合
• 如此重复f+1轮，最终每个正常节点的状态值集合相同，从而很容易选取一个一致的状态值

Proof

用反证法推出矛盾，假设某两个节点在f+1轮之后存活确认，但状态值集合不同，不妨设$ v \in P_i, v \notin P_j $，那么初始状态值为v的节点$P_v$没有活过第一轮，否则在这一轮中，$P_j$会收到来自它的消息，矛盾。然而最终v出现在了$P_i$中，因此v的火种在每一轮都有存活节点保留了下来，然而如果某个节点在第i轮收到了包含v的消息，那么它必然活不过第i+1轮，否则在第i+1轮中，它会给$P_j$发送一个带v的消息，这与$v \notin P_j$矛盾。综上所述，每一轮中都至少有一个带v的节点挂掉，因此fail节点的总数大于f，矛盾。

FLP Proof

终于要谈到重点了，这个证明由 Michael J. Fischer, Nancy Lynch, Mike Paterson 三位科学家给出，发表于1985年的Journal of the ACM.

这个证明说的是，在完全异步的，有单一节点fail的分布式系统中，不存在完全正确的一致性算法。这里有两个重要的概念：

• 完全异步 : 消息的延迟可以是任意长，并且对消息之间的相对速度不做任何假设
• 完全正确 : 假设每个消息延迟上限是单位1的情况下，存在一个有限的N，算法在N个单位的时限内确定停机，停机时所有存活节点的状态相同 (0/1)
  • 需要注意的是这里假设的上限与同步模型中的上限是不同的概念，这里的N应该理解为有因果关系的一组消息的数量，而不是简单的时间

那么根据这些定义，显然在没有节点fail的系统中，完全正确的一致性算法是容易实现的。

More Definitions & Assumptions

• 每个节点的终止状态寄存器只能被修改一次(0/1)，但是中间状态可以有无穷多
• message buffer : 包含了系统中所有被发送但是未传达的消息
• send(P, m) : 将目标节点为P，消息内容为m的消息（内容表示为二者的笛卡尔积）放到buffer
• receive(P) : 尝试从buffer获取目标节点为p的消息，可能返回buffer中存在的消息或者空
• configuration : 全局状态的描述，包括所有节点的当前状态和message buffer中的全部内容
• step : 导致configuration发生变化的源于某个节点P的原子操作，包括如下步骤
  1. receive(P)
  2. 根据p的当前状态和第1步返回的值，修改P的状态
  3. 根据1，2的结果向某些节点发送有限数量的消息
• event : 节点P和receive(P)返回值的二元组， $e = (P, m)$，和其作用的配置一起，完全确定了一个step操作
• schedule : 一个有限或者无限长的可以依次发生的events序列$\delta$
  • run : 与之对应的steps序列
  • $\delta(C)$ : 从configuration C出发，作用了这个调度之后的configuration.
• bivalent : 一个配置C，如果有一个全0的最终配置可达，且有一个全1的最终配置可达，则称其为二阶的，可以理解为配置的不确定性
• 1-valent/0-valent : 只有全1/0的最终配置可达

Lemma 1

如果两个调度$\delta_1, \delta_2$均能作用于配置C，且$\delta_1(C) = C_1, \delta_2(C) = C_2$, 两个调度中发生操作的节点的集合的交为空，那么有$\delta_1(C_2) = \delta_2(C_1) = C_3$。

如图所示:

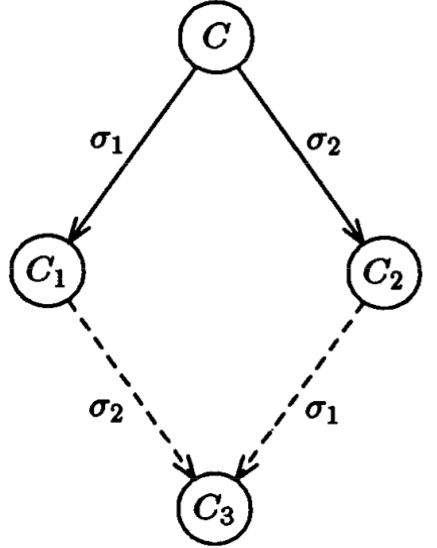
证明：

• 调度1可以作用于C2，调度2可以作用于C1是因为：
  1. 调度1的执行并不会修改调度2中发生操作的节点的状态，也不会取下调度2中取下的消息(目标节点不同)
  2. 同理…
• 两条执行路径的最终配置相同是因为：
  1. 每个event完全确定了一个step的操作
  2. 对于每个发生操作的节点来说，它上面发生的event的次序相同，因此最终配置相同
  3. 对于每个没有发生操作的节点，其状态没有发生变化，均与C保持一致
  4. 从message buffer上取下的消息集合相同
  5. 往message buffer上发送的消息集合相同，根据1

Lemma 2

存在一个bivalent的初始配置。

证明：

1. 反证法，假设所有初始配置不是1-valent就是0-valent，且其中既有1-valent，也有0-valent，否则为平凡解，失去意义
2. 将初始配置中所有节点的初始状态编码为一个二进制数，以格雷码的形式将所有可能的二进制数(i.e.初始配置)排序，相邻的两个数仅有1bit的区别(i.e.只有一个节点的初始状态不同)。
3. 那么排序后必然有一个1-valent的配置与0-valent的配置相邻，设它们的区别在于节点P
4. 考虑到它们在节点P fail的情况下，会进入相同的终止配置，而其中一者为全1，一者全0，矛盾

Lemma 3

从一个bivalent的配置C出发，对于其所有可达配置，如果从C到达该配置的最后一个event是一个可以作用在C上的event e，则称该配置属于集合$S_D$，该集合中存在一个bivalent的配置。

这个定理说的是：从一个不确定的配置C触发，不论作用什么样的event，也无法立即进入一个确定的配置，换句话说，任给一个有限的N，可以找到一个长度大于N的event序列，它作用在C上之后得到的配置依然是一个不确定的配置，从而证明了完全正确的一致性算法是不存在的。

为了证明Lemma 3, 我们需要用反证法证明如下事实：

1. 假设从C触发可达的配置中所有没有发生事件e的配置的集合为$S_C$，则e可以作用在其中的任意配置，且有 $S_D = \{e(C’) | C’ \in S_C\}$
   • 根据消息延时可以任意长的特性，容易证明
2. 假设$S_D$中不包含bivalent配置，则其中既有1-valent又有0-valent的配置
   • 因为C是bivalent的，所以对于$i = 0, 1; \exists E_i$，Ei为从C可达的i-valent的配置
   • 如果Ei恰好在$S_D$中，则满足
   • 否则，$E_i \in S_C, e(E_i) \in S_D$，其中$e(E_i)$必然也是i-valent的(从一个确定的配置出发的所有可达的配置都是同样确定的)
3. $\exists C_0, C_1 \in S_C, e(C_0) = D_0, e(C_1) = D_1$ 其中Di是i-valent，而且Ci之间可以通过单一的事件e’转变。
   • 不失一般性，假设e(C)是0-valent，由于C可以到达D中一个1-valent的配置，设其对应的$S_C$中的配置为C’
   • 考虑从C到C’的调度，其起始配置与D中一个0-valent的配置对应，其终止配置与D中一个1-valent的配置对应
   • 那么这个调度中必然至少存在一个event，其执行前后发生了跳变，取这个event作为e’，前后配置作为Ci即可

接下来考虑e和e’所作用的节点P, P’是否相同，

• 不同，根据Lemma 1，有下图，得出矛盾 (D0 –> D1)。

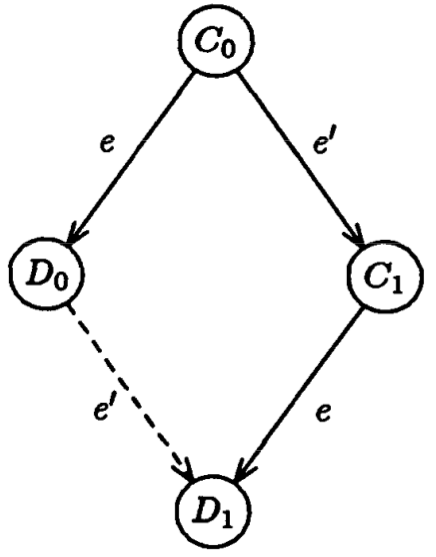
• 相同，取一个从$C_0$可达的终止配置A，$\delta(C_0) = A$，节点P在调度$\delta$中fail，则根据Lemma 1，有下图，可以看到终止配置A可以到达i-valent(i = 0, 1)的配置，这与终止配置的一致性要求矛盾。

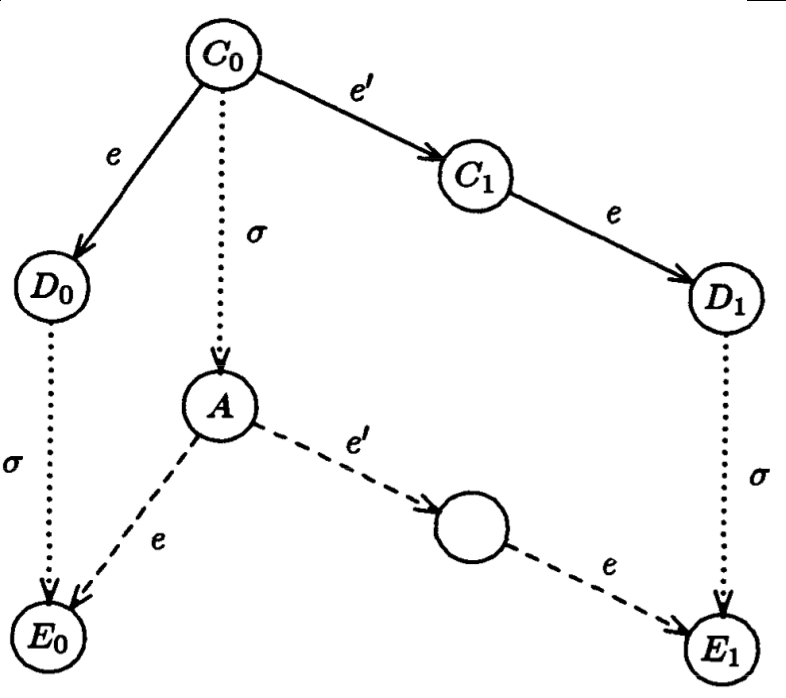
Conclusion

FLP的证明并不意味着一致性算法的研究失去了意义，也不意味着一致性在实际应用中不存在，只是说明了在特定的约束条件下，某种理想效果的不可能。事实上如果我们放宽liveness要求，便可以获得如Paxos这样的算法的支持。

PS: 之所以做这种毫无技术含量的翻译，一方面是出于笔记整理的需求，另外我看到许多对这个证明的解读都或多或少有无法自圆其说的地方（我并不是说我的解读就是天衣无缝，但至少我信了），更重要的是，我实在也没啥有技术含量的东西能分享的…

References

• Consensus_(computer_science))
• Paxos_(computer_science))
• Michael J. Fischer, Nancy Lynch, Mike Paterson, “Impossiblity of Distributed Consensus with One Faulty Process”.