2015-09-02

Quosi Newton Methods

Preface

最近在以蜗牛般的速度啃 PRML。第五章提到了拟牛顿法，这玩意我之前大致意会过，并作了一些笔记，然而我完全无法回忆起来，于是翻出之前的笔记重新意会了一遍，顺便更正了之前一些不太正确的理解，总结整理成下文。

Newton’s Method

考虑求自变量 X 为 N 维向量的函数 $f(X)$ 的极值点问题。我们知道高中数学中的牛顿法可以用于求解函数0点的：$X_{k+1} = X_n - [J_f(X_k)] ^{-1}f(X_k)$. 那么可导函数的极值问题其实就是求其导函数的0点问题，同样可以用牛顿法求解。

以同样的迭代方式逼近，设 $X_k$ 为当前对极值点的估计，考虑 f 在其附近的二阶 Taylor 展开：

$$
f(X) \approx f(X_k) + \nabla f(X_k) \cdot (X - X_k) + 0.5 \cdot (X - X_k) ^T \cdot \nabla ^2 f(X_k) \cdot (X - X_k)\tag{1}\label{eq1}
$$.

引入如下的简化标记（梯度向量，Hessian 矩阵）：

$$
\nabla f = g =
\begin{pmatrix}
\frac{\partial f}{\partial x_1} \\
\frac{\partial f}{\partial x_2} \\
\vdots \\
\frac{\partial f}{\partial x_N} \\
\end{pmatrix} \\
$$

$$
\nabla ^2 f = H =
\begin{pmatrix}
\frac{\partial ^2 f}{\partial x_1 ^2} & \frac{\partial ^2 f}{\partial x_1\partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x_1\partial x_N}\\
\frac{\partial ^2 f}{\partial x_2\partial x_1} & \frac{\partial ^2 f}{\partial x_2 ^2} & \cdots & \frac{\partial ^2 f}{\partial x_2\partial x_N}\\
\vdots & \vdots & \ddots & \vdots\\
\frac{\partial ^2 f}{\partial x_N\partial x_1} & \frac{\partial ^2 f}{\partial x_N\partial x_2} & \cdots & \frac{\partial ^2 f}{\partial x_N ^2}\\
\end{pmatrix}
$$

$\eqref{eq1}$ 的约等号两边分别对 X 求梯度，得到 $\nabla f(X) = g_k + H_k \cdot (X - X_k)$, 我们希望它的值为0，解出对应的 X，作为极值点的下一个估计 $X_{k+1} = X_k - H_k ^{-1} \cdot g_k$.

Wolfe Conditions

在拟牛顿法中，实际的更新并不是严格按照上边的等式进行。为了保证每一步迭代之后，估计点更加逼近极值点（此处以极小值为例），我们采取一种 line search 的方法：$X_{k+1} = X_k - \lambda H_k ^{-1} \cdot g_k$，不改变其更新的方向，但是调整更新步长。这里的参数 α 需要满足所谓的 Wolfe 条件：

$f(\mathbf{X}_k+\lambda\mathbf{p}_k)\leq f(\mathbf{X}_k)+c_1\lambda\mathbf{p}_k ^{\mathrm T}\nabla f(\mathbf{X}_k)$
$\mathbf{p}_k ^{\mathrm T}\nabla f(\mathbf{X}_k+\lambda\mathbf{p}_k) \geq c_2\mathbf{p}_k ^{\mathrm T}\nabla f(\mathbf{X}_k)$

其中 $\mathbf{p}_k = - H_k ^{-1} \cdot g_k$ 称作牛顿方向，$0 < c1 < c2 < 1$, 简单用自然语言解释下上面两个条件：

迭代之后的函数值确实减小了（此处考虑极小值问题，所以牛顿方向需要满足 $p_k ^T g_k < 0$），且至少以线性速率递减，c1 通常取一个很小的数，如 0.0001
每次迭代之后，梯度以近似指数的速率缩小（考虑到两边均小于0），因而能向0趋近，c2 为衰减速率，因而取一个近似1的较大值即可，如 0.9

这样的性质固然很好，但是如何寻找满足如此复杂条件的步长呢？似乎并没有什么高效的办法。所以实际应用中，这个问题往往被近似为 $argmin_{\lambda} f(X_k + \lambda \mathbf{p}_k)$，这将容易数值求解。

此外 Wolfe 条件被证明能够保留 Hessian 矩阵的估计值（将在后文出现）的正定性。

Secant Equation & Quosi-Newton Condition

考虑梯度函数在 $X_k$ 处的一阶泰勒展开，有 $\nabla f(X_k+\Delta X) \approx \nabla f(X_k)+H(X_k) \Delta X$，这被称作 Secant 等式，对应与牛顿法类似的 Secant Method. 当步长足够小时，上式的直接推论： $g_{k+1} - g_k = H_{k+1} \cdot (X_{k+1} - X_k)$，这被称为拟牛顿条件（Quosi-Newton condition）后面的拟牛顿法将利用这个等式来迭代地计算 H，从而降低复杂度。

Broyden–Fletcher–Goldfarb–Shanno algorithm

首先总结下牛顿法的求解思路：

给定初值 $X_0$ 和精度阈值e，k=0
计算 $g_k, H_k$
若 $||g_k|| < e$ 停止，否则计算牛顿方向 $\mathbf{p}_k = - H_k ^{-1} \cdot g_k$
利用牛顿方向计算最优步长因子，$argmin_{\lambda} f(X_k + \lambda \mathbf{p}_k)$
k++, goto step 2

牛顿法的问题就是第二步的数值计算十分低效，PRML 的第五章花了不少篇幅讲解了在神经网络这样特殊的场景下如何利用 back propagation 高效的计算 Jacobian 和 Hessian 矩阵。

一般场景下的做法是通过 Secant 等式来近似地迭代更新 Hessian 矩阵（或者其逆矩阵），于是步骤2的计算代价被大大降低，这样的方法称为 Quosi-Newton Method.

由于篇幅的原因（其实是我懒得抄数学公式），我直接跳过比较古老的 DFP 算法，直接介绍如今比较流行的 BFGS 和 L-BFGS.

引入如下记号：

$s_k = X_{k+1} - X_k$
$y_k = g_{k+1} - g_k$
$B_k \approx H_k$

假设每次迭代更新时，H 的增量满足如下形式 $\Delta B_k = \alpha uu ^T + \beta vv ^T$. 至于为何假设为这样的形式，我估计是出于以下考虑：

如果高阶导数均连续，则 H 矩阵为对称矩阵，参见 Clairaut’s theorem
保留正定性
碰巧有满足拟牛顿条件的特殊解： $\Delta B_k = \frac{y_k y_k ^T}{y_k ^T s_k} - \frac{B_k s_k s_k ^T B_k}{s_k ^T B_k s_k}$

但是计算 H 的目标事实上是为了计算牛顿方向，这需要涉及到矩阵求逆运算，幸运的是，上面的迭代公式可以通过 Woodbury formula 的特殊形式 Sherman–Morrison formula 巧妙地转化为其逆矩阵的迭代公式：

$$B_{k+1} ^{-1} = \left (I-\frac { s_k y_k ^T} {y_k ^T s_k} \right ) B_{k} ^{-1} \left (I-\frac { y_k s_k ^T} {y_k ^T s_k} \right )+\frac {s_k s_k ^T} {y_k ^T \, s_k} \\
= B_k ^{-1} + \frac{(\mathbf{s}_k ^{\mathrm{T}}\mathbf{y}_k+\mathbf{y}_k ^{\mathrm{T}} B_k ^{-1} \mathbf{y}_k)(\mathbf{s}_k \mathbf{s}_k ^{\mathrm{T}})}{(\mathbf{s}_k ^{\mathrm{T}} \mathbf{y}_k) ^2} - \frac{B_k ^{-1} \mathbf{y}_k \mathbf{s}_k ^{\mathrm{T}} + \mathbf{s}_k \mathbf{y}_k ^{\mathrm{T}}B_k ^{-1}}{\mathbf{s}_k ^{\mathrm{T}} \mathbf{y}_k}
$$

这样的计算是非常高效的，并且没有需要存储的中间结果矩阵。

将上述牛顿法算法中的第2-3步中计算牛顿方向的方式换成 $\mathbf{p}_k = - B_{k} ^{-1} \cdot g_k$, 同时加入对 B 的迭代，即得到完整的 BFGS 算法。注意，此处的梯度依然是通过普通方法计算（解析解或者数值解）。

L-BFGS

考虑到当自变量的维度 N 过大时，存储 $B_k ^{-1}$ 需要过多的存储资源，于是便有了 L-BFGS 这样的改版算法，在该算法中，并不存储完整的 Hessian 矩阵的逆矩阵的近似值，而是通过存储 2m 个 N 维向量（最近m 个 s 和 y）来近似还原它。如果令：

$\rho_k = \frac{1}{y_k ^Ts_k}$
$V_k = I - \rho_ky_ks_k ^T$
$D_k = B_k ^{-1}$

反复利用 BFGS 的递推公式可以得到：

$$D\_{k+1} = (V\_k ^TV\_{k-1} ^T \cdots V\_{k-m+1} ^T)D\_{k-m+1}(V\_{k-m+1} \cdots V\_{k-1}V\_k) \\\\ + (V\_k ^TV\_{k-1} ^T \cdots V\_{k-m+2} ^T)(\rho\_{k-m+1}s\_{k-m+1}s\_{k-m+1} ^T)(V\_{k-m+2} \cdots V\_{k-1}V\_k) \\\\ + (V\_k ^TV\_{k-1} ^T \cdots V\_{k-m+3} ^T)(\rho\_{k-m+2}s\_{k-m+2}s\_{k-m+2} ^T)(V\_{k-m+3} \cdots V\_{k-1}V\_k) \\\\ + ... \\\\ + (V\_k ^TV\_{k-1} ^T)(\rho\_{k-2}s\_{k-2}s\_{k-2} ^T)(V\_{k-1}V\_k) \\\\ + V\_k ^T(\rho\_{k-1}s\_{k-1}s\_{k-1} ^T)V\_k \\\\ + \rho\_ks\_ks\_k ^T$$

于是只需要对 $D_{k-m+1}$ 作出估计即可近似地计算出牛顿方向，通常取 $D_{k-m+1} = \frac{s_k ^T y_k}{y_k ^T y_k} I$.

Conjugate Gradient Method

既然提到了拟牛顿法，就顺便提一下另一种高效的非线性优化算法——共轭梯度法。

Steepest Gradient Descent

最 Naive 的非线性优化思路是：

寻找函数在点 X 的梯度 $\nabla f(X)$
沿梯度反方向作 line search，寻找更新步长 $argmin_{\lambda} f(X - \lambda \nabla f(X))$
根据2的结果更新 X，重复1-2直至收敛

这个算法的低效源于：在极值点附近，梯度方向往往并不指向极值（存在某种形变），对应与下图中的绿色折线。

sgd

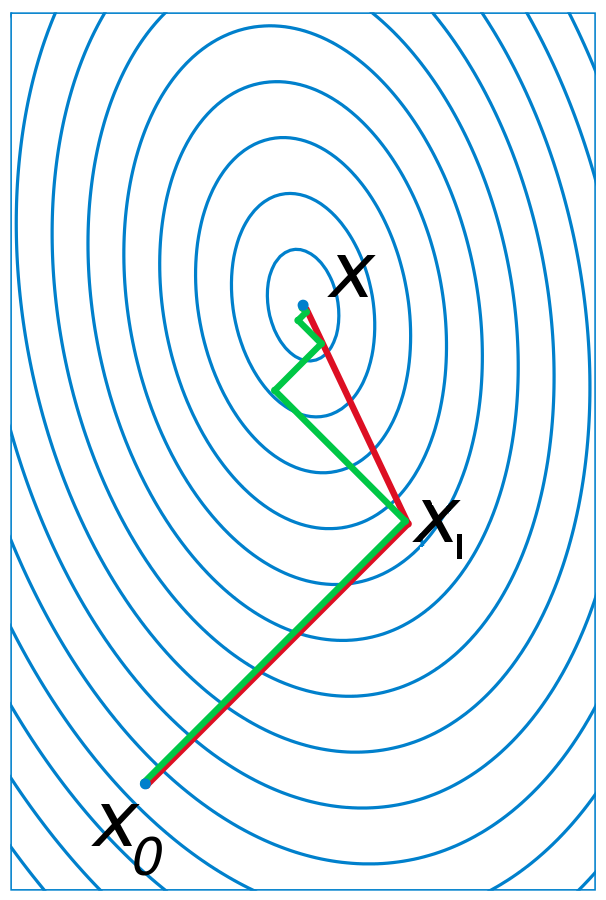
所以共轭梯度法的基本思路就是将这样的形变考虑在内，通过变化更新方向来抵消影响, 如上图中的红线。

Approximate Linear Equation

由于任意的二阶可导函数在极值点附近近似为一个二次型（通过泰勒展开容易得到），而这样的二次型近似可以大致捕获上边描述的形变，因此我们首先来考虑二次型的极小值问题：

$$
f(X) = \frac12 X ^\mathrm{T} \mathbf{A}X - X ^\mathrm{T} \mathbf{b} , \quad X\in\mathbf{R} ^n.
$$

令其梯度为0，我们得到极值点方程：

$$
\mathbf{AX_*} = \mathbf{b}\tag{2}\label{eq2}
$$.

A-conjugate Vectors

将向量的内积进行扩展，定义 A-dot: $\mathbf{u}^\mathrm{T} \mathbf{A} \mathbf{v}$. 向量 u, v 被称为 A-conjugate iff 其 A-dot 为零，或称 A-orthogonal, 显然这个二元关系满足交换律。下面考虑这个定义在上述优化问题中的意义。

设 $X_*$ 为待求的上述目标函数的极小值点，则 $f(X) = \frac12 (X - X_*) ^{\mathrm{T}} \mathbf{A} (X - X_*)$

考虑极值点附近的等势图（如上图），对于 $X_1$，它是从 $X_0$ 出发作 line search 之后得到的最小值点，则向量 $\mathbf{u} = X_1 - X_0$ 必与某个等势线相切，$X_1$ 为切点。由于该处的梯度向量为 $\nabla{f(X_1)} = \mathbf{A} (X_1 - X_*) = \mathbf{A v}$，得到相切关系方程：$\mathbf{u}^\mathrm{T} \mathbf{A} \mathbf{v} = 0$. 换句话说，沿某个方向（如梯度反方向）找到极小值点之后，下一步更新的方向应该选其共轭方向。对于二维，二次型函数，这样的两步更新必能找到极值点；同理对于 N 维的情形，只需 N 步，更新方向两两共轭，这一点稍后会简要分析。

所以，从上面的分析可以看出，共轭方向的实质是引导更新方向重新指向极值点，从而减少更新步骤，提高效率。那么接下来的问题是：

如何选择共轭方向？
如何计算每一步的更新步长？

Iterative Method

首先，不失一致性（座标平移），设 $X_0 = 0$. 下面回答上边提出的两个问题：

方向选择
1. 初始时，我们选取的更新方向为 $\mathbf{p}_0 = -\nabla{f(X_0)} = \mathbf{b} - \mathbf{A} X_0$，
2. 之后将依次选择接近于 $\mathbf{r}_k = \nabla{f(X_k)}$, 且与之前的更新方向均共轭的方向 $\mathbf{p}_k$
3. 更新的方法类似于正交基的选取，$\mathbf{p}_{k} = \mathbf{r}_{k} - \sum_{i < k}\frac{\mathbf{p}_i ^\mathrm{T} \mathbf{A} \mathbf{r}_{k}}{\mathbf{p}_i ^\mathrm{T}\mathbf{A} \mathbf{p}_i} \mathbf{p}_i$, 即需要从负梯度方向中减去它在之前各个更新方向中的 A-projection. 参见 Gram–Schmidt process.
更新步长
1. 由于初始点选为 0 点，所以有 $X_k = \sum\limits_{i < k} \lambda_k \mathbf{p}_k$, 于是 $\mathbf{p}_k ^{\mathrm{T}} \mathbf{A} X_k = 0$. 即每一步的更新方向与此刻 X 所在的方向共轭。
2. 计算 $argmin_{\lambda_k} - \frac12 (X_k + \lambda_k \mathbf{p}_k) ^{\mathrm{T}} A (X_k + \lambda_k \mathbf{p}_k) + \mathbf{b}(X_k + \lambda_k \mathbf{p}_k)$
3. 令上式对 $\lambda_k$ 的偏导为0，并结合1中得出的共轭结论，容易得到更新步长的解析解：

$$
\lambda_{k} = \frac{\mathbf{p}_k ^\mathrm{T} \mathbf{b}}{\mathbf{p}_k ^\mathrm{T} \mathbf{A} \mathbf{p}_k} = \frac{\mathbf{p}_k ^\mathrm{T} (\mathbf{r}_{k-1}+\mathbf{Ax}_{k-1})}{\mathbf{p}_{k} ^\mathrm{T} \mathbf{A} \mathbf{p}_{k}} = \frac{\mathbf{p}_{k} ^\mathrm{T} \mathbf{r}_{k-1}}{\mathbf{p}_{k} ^\mathrm{T} \mathbf{A} \mathbf{p}_{k}}
$$

根据上式可以看出，每一步的更新量为向量 b 在 $\mathbf{p}_k$ 方向上的 A-projection. 恰好初始点为0，又极值点满足 $\eqref{eq2}$, 因此各个更新量正好构成了 $X_*$ 在 ${\mathbf{p}_k}$ 这组共轭正交基上的分解，因此只需至多 N 步更新即可找到极值点，具体的形式化推导参见维基百科。

Tuning

上面的算法存在的问题在于，计算新方向时，需要记录各个共轭方向的历史信息，当 N 很大时，消耗过多的存储资源，因此共轭梯度法在实际应用时采用某种近似的手段来进行优化，使得只需要记录最近一次的3个向量$X_k, \mathbf{p}_k, \mathbf{r}_k$，如 Fletcher–Reeves 算法，其推导及相关公式参见维基百科。对于一般的非线性优化问题，通用的算法框架如下：

计算负梯度方向
根据 Fletcher-Reever 公式（或其它变种）计算方向变化量
根据1,2的结果以及“上一个共轭方向”计算新的共轭方向
在新的方向上作 line search 找到合适步长
更新 X
重复 1-5 直至收敛

与拟牛顿法相较而言，共轭梯度法的收敛速度要慢一些，但依然比普通的梯度下降法要迅速得多，因而不失为一个好的选择。而且由于它所需的存储资源远小于拟牛顿法（即便是 L-BFGS 也需要 O(2mN)), 格外适用于维度极大的优化问题。

Don't Panic!