Hammersley Clifford Theorem
Preface
PRML 中 8.3.2 小节简单描述了 Markov Random Fields 的分解特性,其中最核心的部分就是 Hammersley Clifford Theorem, 然而它并没有证明这个定理,只是在末尾的时候提到了这个结论,导致我在阅读中间部分的时候一头雾水。好在我 google 到了一个优雅的证明,顺便翻译在此。
Probabilistic Graphical Models
先随便插点 PRML 中关于概率图模型比较重要的论述。
- 概率图模型用于形象地描述一组随机变量的联合分布
- 可以被看作是对联合分布的一种过滤器
- 如果图 G 中反映出的所有变量间的条件独立性质均在某个分布 P 中满足,则 P 可以通过该过滤器
- 在满足上一条的前提下,如果 P 中真实存在的所有变量间的条件独立性在图 G 上均能反映,则称 G 为 P 的 perfect map
- 概率图模型大致分为两种,有向图和无向图
- 有向图的优点在于联合分布可以很容易地分解为节点属性(也就是条件概率)的乘积
- 然而有向图在反映条件独立性质的时候,并不十分直接(head-2-head)
- 无向图可以直观地反映变量间的条件独立性质,代价是联合分布较难表示,而后文将证明的定理就是为了解决这个问题
- 有向图和无向图的表达能力是不同的
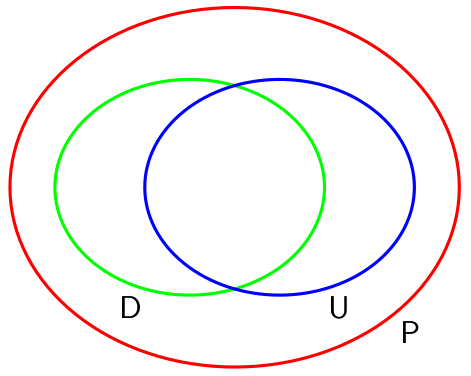
- 换句话说,给定随机变量集合后,能够用有向图 perfect map 的所有联合分布的集合 D 与能够用无向图 perfect map 的所有联合分布的集合 U 并不相同
- 它们与所有该随机变量集合能够形成的联合分布集合 P 的关系如下图:
Markov Random Fields
- 无向图模型
- 图中的每个节点对应一个或一组随机变量
- 图中的连线表示随机变量之间的联系,具有如下属性:
- 变量间的条件独立性容易判断,事实上,假设 A, B, C 为图 G 中的3组顶点集合
- 如果 A 到 B 的每条路线中都至少经过 C 中的一个顶点,则称 A 与 B 在条件 C 下独立
- 记作 $A \perp\!\!\!\perp B | C$,满足:
$$
P(A, B | C) = P(A | C) \cdot P(B | C)\tag{0}\label{eq0}
$$
- 考虑顶点 $X_i$, 记其所有邻顶点集合为 $N_i$, 令 $D_i = N_i \cup \{X_i\}, A = \{X_i\}, B = G/D_i, C = N_i$
- B 为图中除去顶点 i 及其相邻顶点后的集合,C 为其邻顶点集,A 与 B 中的连线必过 C,于是 $P(X_i, X_{G/D_i} | X_{N_i}) = P(X_i | X_{N_i}) P(X_{G/D_i} | X_{N_i})$
- 根据贝叶斯公式
$$
P(X_i | X_{G/i}) = \frac{P(X_i, X_{G/D_i} | X_{N_i})}{P(X_{G/D_i} | X_{N_i})} = \frac{P(X_i | X_{N_i}) P(X_{G/D_i} | X_{N_i})}{P(X_{G/D_i} | X_{N_i})} = P(X_i | X_{N_i})\tag{1}\label{eq1}
$$
换句话说,$X_i$ 的条件概率,仅与其相邻顶点的取值相关。以上便是 MRF 的定义。
Gibbs Distribution
- 一个定义在无向图 G 上的联合概率分布 $P(X)$ 被称为 Gibbs 分布 iff:
- 它能够被分解为关于 G 中的团(联通子图)的正函数的积
- 记 $C_G$ 为图 G 中所有团的集合,$Z = \sum_x \prod_{c \in C_G} \phi_c(X_c)$ 为归一化因子,即有:
$$
P(X) = \frac1Z \prod\limits_{c \in C_G} \phi_c(X_c)\tag{2}\label{eq2}
$$
注意到团上的函数之积可以合并,我们可以将 $C_G$ 定义为最大团集合,表达能力不变。
Hammersley Clifford Theorem
该定理说的是,MRF 与 Gibss 分布的定义等价。i.e. 对于同样的 G,上述两种定义能够表示的所有联合概率分布 $P(X)$ 的集合相同。下面给出该定理的证明。
Backward Direction
先证明:Gibbs 分布满足 MRF 中通过拓扑引入的所有条件独立特性, 即满足 $\eqref{eq1}$.
通过边缘分布公式,有:
$$
P(X_i | X_{N_i}) = \frac{P(X_i, X_{N_i})}{P(X_{N_i})} = \frac{\sum_{G/D_i} \prod_{c \in C_G} \phi_c(X_c)}{\sum_{x_i}\sum_{G/D_i} \prod_{c \in C_G} \phi_c(X_c)}\tag{3}\label{eq3}
$$
然后将 $C_G$ 中的团,依据是否包含 $X_i$ 分为两类:
- $C_i = \{c \in C_G : X_i \in c\}$
- $R_i = \{c \in C_G : X_i \notin c\}$
于是将 $\eqref{eq3}$ 中的分子分母均进行分解,得到:
$$
P(X_i | X_{N_i}) = \frac{\sum_{G/D_i} \prod_{c \in C_i} \phi_c(X_c) \prod_{c \in R_i} \phi_c(X_c)}{\sum_{x_i}\sum_{G/D_i} \prod_{c \in C_i} \phi_c(X_c) \prod_{c \in R_i} \phi_c(X_c)} = \frac{\prod_{c \in C_i} \phi_c(X_c) \sum_{G/D_i} \prod_{c \in R_i} \phi_c(X_c)}{\sum_{x_i} \prod_{c \in C_i} \phi_c(X_c) \sum_{G/D_i} \prod_{c \in R_i} \phi_c(X_c)} \tag{4}\label{eq4}
$$
之所以能够交换求和号与求积号的顺序,是因为 $C_i$ 中的团 c 包含了 $X_i$, 于是 c 中的所有顶点均在 $D_i$ 中,因此求和过程中 $\prod_{c \in C_i} \phi_c(X_c)$ 保持不变。又 $\sum_{G/D_i} \prod_{c \in R_i} \phi_c(X_c)$ 与 $x_i$ 无关,因此可以被约去,得到:
$$
P(X_i | X_{N_i}) = \frac{\prod_{c \in C_i} \phi_c(X_c)}{\sum_{x_i}\prod_{c \in C_i} \phi_c(X_c)} = \frac{\prod_{c \in C_i} \phi_c(X_c)}{\sum_{x_i}\prod_{c \in C_i} \phi_c(X_c)} \cdot \frac{\prod_{c \in R_i} \phi_c(X_c)}{\prod_{c \in R_i} \phi_c(X_c)}\\
= \frac{\prod_{c \in C_G} \phi_c(X_c)}{\sum_{x_i}\prod_{c \in C_G} \phi_c(X_c)} = \frac{P(X)}{P(X_{G/{i}})} = P(X_i | X_{G/i})
$$
即得 $\eqref{eq1}$.
Forward Direction
需要证明:如果 $\eqref{eq1}$ 成立,则存在这样的 $\phi_c(X_c)$ 使得 $\eqref{eq2}$ 成立。通过构造加以证明,首先定义子集 $s \subset G$ 上的函数:
$$
f_s(X_s = x_s) = \prod\limits_{z \subset s} P(X_z = x_z, X_{G/z} = 0) ^{-1 ^{|s| - |z|}}
$$
该函数为所有 s 的子集 z 上的函数之积,$P(X_z = x_z, X_{G/z} = 0)$ 对应于 z 中元素与给定的取值相同,其余元素全为 0 的概率。当 z 与 s 的大小相差为偶数时,对应的指数为1,否则为-1.
容易直到,如果能够证明如下两个性质,则 $\phi_c(X_c) = f_c(X_c)$ 即满足条件。
- $\prod_{s \subset G} f_s(X_s) = P(X)$
- 若 s 不是团,则 $f_s(X_s) = 1$
对于性质1,考虑某个 $z \subset G$, 考虑 $\Delta = P(X_z, X_{G/z} = 0)$ 在1的左边出现的所有因子。它在 $f_z(X_z)$ 中出现过,对应的指数为 1,对应的因子为 $\Delta$; 又它出现在 $C_{|G| - |z|} ^1$ 个“恰包含了 z 以及另1个元素的子集”的函数值中,对应的因子的积为 $\Delta ^{- C_{|G| - |z|} ^1}$; 又它出现在 $C_{|G| - |z|} ^2$ 个“恰包含了 z 以及另外2个元素的子集”的函数值中,对应的因子的积为 $\Delta ^{C_{|G| - |z|} ^2}$ …… 由于 $0 = (1 - 1) ^K = C_K ^0 - C_K ^1 + C_K ^2 + \cdots + (-1) ^K C_K ^K$, 1中左侧各个子集 z 对应的因子的总乘积为1,除非 z 取 G,对应的因子即为 $P(X)$.
接下来,通过 MRF 的属性来证明性质2. 对于 s 非团的情况,取其中不相连的两个顶点 a, b.
$$
f_s(X_s) = \prod\limits_{w \subset s/\{a, b\}} [\frac{P(X_w, X_{G/w}=0)P(X_{w \cup \{a, b\}}, X_{G/w \cup \{a, b\}}=0)}{P(X_{w \cup \{a\}}, X_{G/w \cup \{a\}}=0)P(X_{w \cup \{b\}}, X_{G/w \cup \{b\}}=0)}] ^{-1 ^*}
$$
即考虑 s 中所有子集中 a, b 的出现情况,分为四类,并将对应的因子合并,$-1 ^*$ 表示指数无关紧要,因为紧接着将证明等号右边中每个因子的底数为1. 根据贝叶斯法则:
$$
\frac{P(X_w, X_{G/w} = 0)}{P(X_{w \cup \{a\}}, X_{G/w \cup \{a\}} = 0)} \\
= \frac{P(X_a = 0|X_w, X_b = 0, X_{G/w \cup \{a, b\}} = 0)P(X_w, X_b = 0, X_{G/w \cup \{a, b\}} = 0)}{P(X_a | X_w, X_b = 0, X_{G/w \cup \{a, b\}} = 0)P(X_w, X_b = 0, X_{G/w \cup \{a, b\}} = 0)} \\
= \frac{P(X_a = 0|X_w, X_b, X_{G/w \cup \{a, b\}} = 0)P(X_w, X_b, X_{G/w \cup \{a, b\}} = 0)}{P(X_a | X_w, X_b, X_{G/w \cup \{a, b\}} = 0)P(X_w, X_b, X_{G/w \cup \{a, b\}} = 0)} \\
= \frac{P(X_{w \cup \{b\}}, X_{G/w \cup \{b\}} = 0)} {P(X_{w \cup \{a, b\}}, X_{G/w \cup \{a, b\}} = 0)} \tag{5}\label{eq5}
$$
上式中第二的等式成立是因为:
- 分子分母的右侧因子相同,同时进行了替换
- 取 $A = \{a\}, B = \{b\}, C = G/\{a, b\}$,由 $A \perp\!\!\!\perp B | C$ 以及 $\eqref{eq0}$ 得到 $P(A | B, C) = \frac{P(A, B | C)}{P(B | C)} = P(A | C) = P(A | B = b, C)$ 即 $P(X_a | X_w, X_b = 0, X_{G/w \cup \{a, b\}} = 0) = P(X_a | X_w, X_b, X_{G/w \cup \{a, b\}} = 0)$, 同理分子的部分也相等。
根据 $\eqref{eq5}$ 容易得到性质2,于是正向的证明完成。