Fisher information and CRLB
Fisher Information
又来抄录 Wikipedia 了,Fisher information 这个词我在好多地方见过,一直是不求甚解地意会着,最近发现这影响到一些东西的理解,于是开始翻看百科。
言归正传,Fisher information 对于学统计的人应该很熟悉,用于描述可观测的变量 X 包含的对于决定它分布的参数 $\theta$ 的信息大小,直观地理解,如果 X 包含的关于 $\theta$ 的信息越多,后者就越确定,也就是其估计的方差越小。了解到这个信息就能得知,对于某些特定的分布模型,我们对于参数 $\theta$ 的极大似然估计 $\hat{\theta}_{ML}$ 的确信程度。
更加精确地:
- X 是一个可观测的随机变量
- X 的分布由未知参数 $\theta$ 决定
- 似然函数(likelihood function) 表示为 $f(x; \theta) = P(x | \theta)$
Fisher information 的定义如下:
$$
\mathcal{I}(\theta)=\operatorname{E} \left[\left. \left(\frac{\partial}{\partial\theta} \log f(X;\theta)\right) ^2\right|\theta \right] = \int \left(\frac{\partial}{\partial\theta} \log f(x;\theta)\right) ^2 f(x; \theta)\; \mathrm{d}x \\
= - \operatorname{E} \left[\left. \frac{\partial ^2}{\partial\theta ^2} \log f(X;\theta)\right|\theta \right] \tag{1}\label{eq1}
$$
后一个等号成立是因为:
$$
\frac{\partial ^2}{\partial\theta ^2} \log f(X;\theta)=
\frac{\frac{\partial ^2}{\partial\theta ^2} f(X;\theta)}{f(X; \theta)}
\;-\;
\left( \frac{\frac{\partial}{\partial\theta} f(X;\theta)}{f(X; \theta)} \right) ^2=
\frac{\frac{\partial ^2}{\partial\theta ^2} f(X;\theta)}{f(X; \theta)}
\;-\;
\left( \frac{\partial}{\partial\theta} \log f(X;\theta)\right) ^2
\\
\operatorname{E} \left[\left. \frac{\frac{\partial ^2}{\partial\theta ^2} f(X;\theta)}{f(X; \theta)}\right|\theta \right]=\int \frac{\frac{\partial ^2}{\partial\theta ^2} f(x;\theta)}{f(x;\theta)}f(x;\theta)\; \mathrm{d}x=
\frac{\partial ^2}{\partial\theta ^2} \int f(x; \theta)\; \mathrm{d}x=
\frac{\partial ^2}{\partial\theta ^2} \; 1 = 0.
$$
注意:
- X 表示随机变量,而 x 表示该变量的特定取值
- 取期望值的时候 $\theta$ 保持不变,表示其真实值
- 似然函数表示对应的条件概率密度,故 $\int f(x;\theta)\;\mathrm{d}x = 1$
The Intuition
首先来看为什么上边定义的 information 能够表示上边提到的 “X 包含的对于决定它分布的参数 $\theta$ 的信息大小”。
我们知道后验概率 $P(\theta|x) \propto P(x|\theta) P(\theta)$,当先验分布为均匀分布时(即没有任何对参数的先验知识),$P(\theta|x) \propto f(x;\theta)$
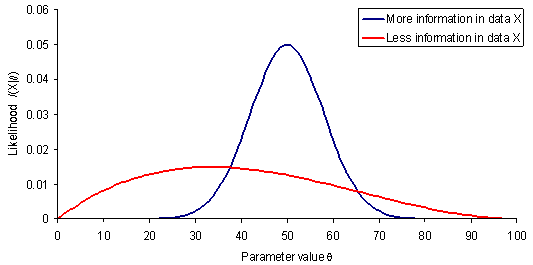
上图中,对于两组特定的样本,其后验概率密度函数的形状与图中的曲线相同,较为陡峭的蓝线在其极大似然的参数 $\hat{\theta}_{ML}$ 附近的变化剧烈,对应了参数较为确定,也就是“X 包含了更多关于参数的信息”。而 Fisher information 恰好能够描述这种陡峭程度,由于:
- 考虑足够多样本的情形,由于 MLE 是 consistent estimator, $\hat{\theta}_{ML} \to \theta$
- 假设 log likelihood 二阶导数的期望近似于 log likelihood 的期望的二阶导数,而后者为一个以 $\theta$ 为极值的函数的二阶导数(在 $\theta$ 处)。
- Fisher information 近似描述了后验概率的 log 期望在 MLE 处的二阶导数的大小,即陡峭程度。
Properties of MLE
顺便提一下有关 MLE (Maximum Likelihood Estimator) 的两个重要属性,这也与 Fisher information 密切相关。
Consistency
说的是,当样本足够多时,MLE 趋近于真实参数值,简单证明如下:
- 与前文标记略有不同,此处令真实的参数值为 $\theta_0$, 且定义
$$
L(\theta) = E_{\theta_0} l(X|\theta) = \operatorname{E} \left[\left. log\ f(X;\theta)\right|\theta_0 \right] = \int (log f(x; \theta)) f(x; \theta_0) \mathrm{d}x
$$ - 根据 MLE 的定义
$$
\hat{\theta}_{ML} = \underset{\theta}{\operatorname{argmax}} L_n(\theta) = \underset{\theta}{\operatorname{argmax}} \frac1n \sum\limits_{i=1} ^n log\ f(x_i; \theta)
$$ - 根据大数定理,有 $L_n(\theta) \to L(\theta)$
- 根据K-L divergence,有 $\underset{\theta}{\operatorname{argmax}} L(\theta) = \theta_0$
- 根据 2,3,4 可得 $\hat{\theta}_{ML} \to \theta_0$
Asymptotic normality
$\sqrt{n}(\hat{\theta}_{ML} - \theta_0) \to ^d N(0, 1/\mathcal{I}(\theta_0))$,在 consistency 的基础上,表明了 MLE 服从高斯分布,其方差为 Fisher information 的倒数。简单证明如下:
- 根据上边的1得到 $L’_n(\hat{\theta}_{ML}) = 0$,同理有 $L’(\theta_0) = E_{\theta_0} l’(X|\theta_0) = 0$
- 不妨设 $\theta_0 \leq \hat{\theta}_{ML}$, 根据微分中值定理
$$
\exists \theta_1 \in [\theta, \theta_0], 0 = L’_n(\hat{\theta}_{ML}) = L’_n(\theta_0) + L’’(\theta_1)(\hat{\theta}_{ML} - \theta_0)
$$ - 于是
$$
\sqrt{n}(\hat{\theta}_{ML} - \theta_0) = - \frac{\sqrt{n}L’_n(\theta_0)}{L’’_n(\theta_1)}
$$ - 根据中心极限定理
$$
\sqrt{n}L’_n(\theta_0) = \sqrt{n}(\frac1n \sum\limits_{i=1} ^ n f’(x_i; \theta_0) - 0) = \sqrt{n}(\frac1n \sum\limits_{i=1} ^ n f’(x_i; \theta_0) - E_{\theta_0}l’(X|\theta_0)) \to N(0, var_{\theta_0}(l’(X|\theta_0)))
$$ - 根据大数定理(LLN)
$$
L’’_n(\theta) = \frac1n \sum l’’(X_i|\theta) \to E_{\theta_0}l’’(X|\theta)
$$
又 $\hat{\theta}_{ML} \to \theta_0, \theta_1 \to \theta_0$,于是
$$
l’’_n(\theta_1) \to E_{\theta_0}l’’(X|\theta_0) = -\mathcal{I}(\theta_0)
$$ - 根据 4,5 可得
$$-\frac{\sqrt{n}L’_n(\theta_0)}{L’’_n(\theta_1)} \to ^d N(0, \frac{var_{\theta_0}(l’(X|\theta_0))}{\mathcal{I}(\theta_0) ^2})
$$ - 又根据 1 以及 $\eqref{eq1}$
$$
var_{\theta_0}(l’(X|\theta_0)) = E_{\theta_0}(l’(X|\theta_0)) ^2 - (E_{\theta_0}l’(X|\theta_0)) ^2 = \mathcal{I}(\theta_0) - 0
$$
再根据 3,6 即得结论
Overview of the Proofs
用一张图表示各个重要结论之间的导出关系:
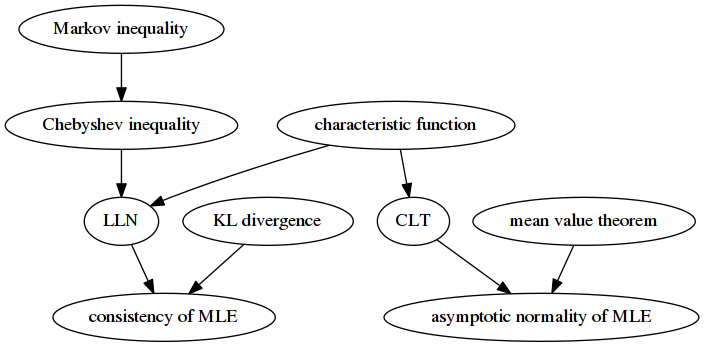
至于具体的证明细节,就不长篇抄袭了……
Cramér–Rao Lower Bound
另一个关于 Fisher information 的重要结论就是 Cramér–Rao inequality:
对于任意的关于 $\theta$ 的无偏估计 $\hat{\theta}$,必然有 $var(\hat{\theta}) \geq 1/\mathcal{I(\theta)}$.
更一般地,若有偏估计 T 满足 $E(T) = \psi(\theta)$,则 $var(T) \geq \frac{\psi’(\theta) ^2} {\mathcal{I(\theta)}}$.
Proof
对上面的一般结论进行简短的证明:
- 令
$$
V = l’(\theta) = \frac{\partial}{\partial\theta} log f(X;\theta) = \frac{f’(X;\theta)}{f(X;\theta)}
$$
有
$$
E(V) = \int_x f(x;\theta)[\frac{1}{f(x;\theta)}\frac{\partial}{\partial\theta}f(x;\theta)] \mathrm{d}x = \frac{\partial}{\partial\theta} \int_x f(x;\theta)\mathrm{d}x = 0
$$ - 根据 1
$$cov(V, T) = E(VT - E(V)T - E(T)V + E(V)E(T)) = E(VT) - E(T)E(V) = E(VT)
$$ - $$
cov(V, T) = E(VT) = \int_x t(x)[\frac{\partial}{\partial\theta}f(x;\theta)] \mathrm{d}x = \frac{\partial}{\partial\theta}[\int_x t(x)f(x;\theta)\mathrm{d}x] = \psi’(\theta)
$$ - 根据柯西-洗袜子不等式
$$
var(T)var(V) \geq cov(V, T) ^2 = \psi’(\theta) ^2
$$ - 根据定义 $\eqref{eq1}$,$var(V) = \mathcal{I}(\theta)$,带入 4 即得结论
Multivariate Extention
论文中出现较多的情况是多参数的 CRLB, 定义如下:
- 参数: $\boldsymbol{\theta} = \left[ \theta_1, \theta_2, \dots, \theta_d \right] ^T \in \mathbb{R} ^d$
- Fisher information matrix 是一个 d x d 的矩阵,元素
$$
I_{m, k}
= \mathrm{E} \left[
\frac{\partial }{\partial \theta_m} \log f\left(x; \boldsymbol{\theta}\right)
\frac{\partial }{\partial \theta_k} \log f\left(x; \boldsymbol{\theta}\right)
\right] = -\mathrm{E} \left[
\frac{\partial ^2}{\partial \theta_m \partial \theta_k} \log f\left(x; \boldsymbol{\theta}\right)
\right].
$$ - 偏估计 $\boldsymbol{T}(X) = (T_1(X), \ldots, T_d(X)) ^T$ 满足 $\mathrm{E}(\boldsymbol{T}(X)) = \boldsymbol{\psi}(\boldsymbol{\theta})$
有结论如下:
$$
\mathrm{cov}_{\boldsymbol{\theta}}\left(\boldsymbol{T}(X)\right) \geq
\frac {\partial \boldsymbol{\psi} \left(\boldsymbol{\theta}\right)}
{\partial \boldsymbol{\theta}} [I\left(\boldsymbol{\theta}\right)] ^{-1}
\left( \frac {\partial \boldsymbol{\psi}\left(\boldsymbol{\theta}\right)}
{\partial \boldsymbol{\theta}}
\right) ^T
$$
证明略过,抄数学公式也是累…
综合 CRLB 以及 MLE 的 Asymptotic Normality 性质,可知当样本足够时,MLE 趋向于最优估计(无偏,且方差最小)。